Home About Basics Casts Theory Verification References Contact

Verification fly rod

Purpose

The purpose of this section is to demonstrate how the rod input, used in the simulation model, is verified.

Method

Each rod is specified by distributions of:

· Outer diameter. The outer diameter is used to calculate air drag.

· Bending stiffness. The bending stiffness gives the relation between bending moment and curvature in static bending. The bending stiffness distribution determines the rod deflection profile when subject to applied static loads (in zero gravity).

· Mass density i.e., mass per unit length. The mass density distribution with the bending stiffness distribution gives dynamic rod properties e.g., eigenfrequencies.

Here, the method used to verify the rod distributions is presented with the rod distributions for the 50ft oh ref. cast as an example. The fly rod blank is modeled for each rod section as a hollow tapered tube with a Young’s modulus and density varying linearly along the section. The outer diameter is measured but the inner diameter, Young’s modulus and density are treated as unknowns. The unknowns are varied until acceptable agreement with experiments is obtained.

Each ferrule gives an increase in local bending stiffness and mass density.

The guides (including wrapping) give additions to the mass density with the relative additions being largest for the tip section. The guides are modeled using a smoothed mass density distribution giving an addition centered at the position of each guide.

The rod verification method includes the following measurements:

1. Rod tip deflection for applied loads.

2. Mass for rod sections (zero moment mass distribution).

3. Position for center of mass for rod sections (first moment mass distribution).

4. Frequency of small amplitude physical pendulum oscillations (second moment mass distribution).

5. First eigenfrequency for clamped rod vibrations (small amplitude).

The measurements listed above were made for:

· the rod top section only.

· The rod top section + 1 section.

· The rod top section + 2 sections.

· The complete rod above the handle (measurements 2, 3 and 4 not applicable).

Used equipment:

· Mass measurements were made using a precision gauge, resolution 0.001 g, accuracy 0.01 g.

· Deflections (on rod sections) were measured using a digital caliper, resolution 0.01 mm, estimated accuracy 0.25 mm.

· Deflections (large, on complete rod) were measured using a ruler, estimated accuracy 1 mm.

· Tip angles were measured using a protractor, estimated accuracy 1 deg.

· Eigenfrequencies were measured using video (240 frames per second) counting 30 cycles, estimated accuracy 0.1%.

· Physical pendulum frequencies were measured using video (60 frames per second) counting 10 cycles, estimated accuracy 0.3%.

· Fixations during measurements were done using clamps and wooden blocks. Measurements on the complete rod were done using a “3-point fixture for the rod handle”, shown schematically below:

Measurements on rod sections were done using wooden blocks with semicircular grooves, shown schematically below:

The static deflections were measured and calculated as the vertical differences between tip positions for the unloaded and loaded rod tip, see example showing the top section in the figure below:

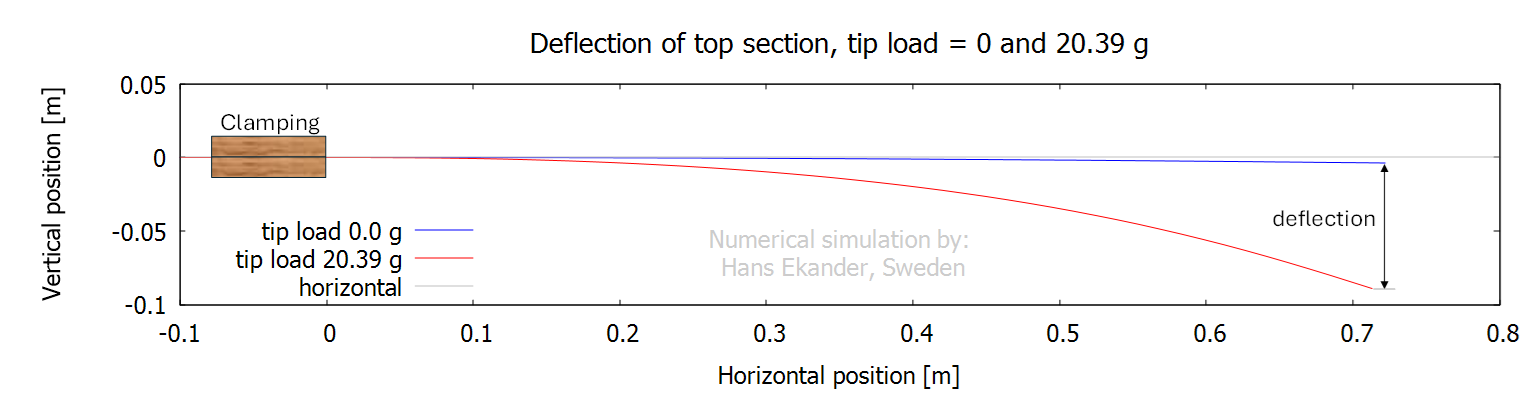
Note: The deflection due to gravity of the unloaded top section gives a vertical tip deflection of 3.7 mm. The corresponding figure the complete unloaded rod is about 52 mm.

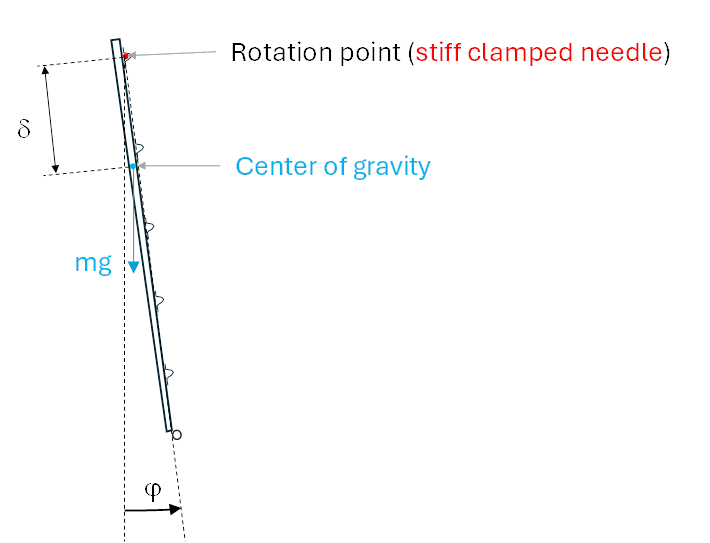
The period for small amplitude oscillations of a physical pendulum (here rod section(s)) is a function of the moment of inertia around the rotation point and the restoring torque per unit angle, mgd. It was measured with the rotation point defined by a needle as sketched below:

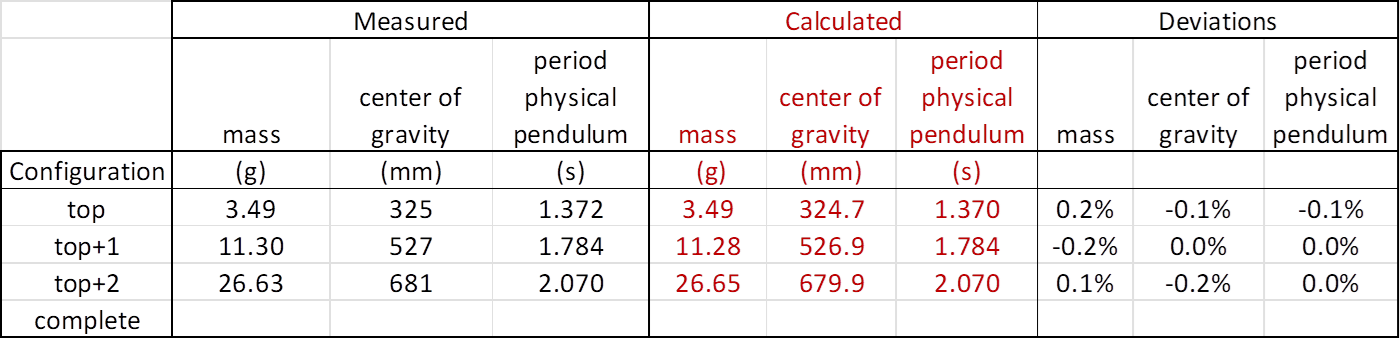
Results, mass distribution:

The outer diameter comparisons are trivial and are not presented here. Comparisons of experimental data and input to the simulation model for the mass distributions are shown in the table below:

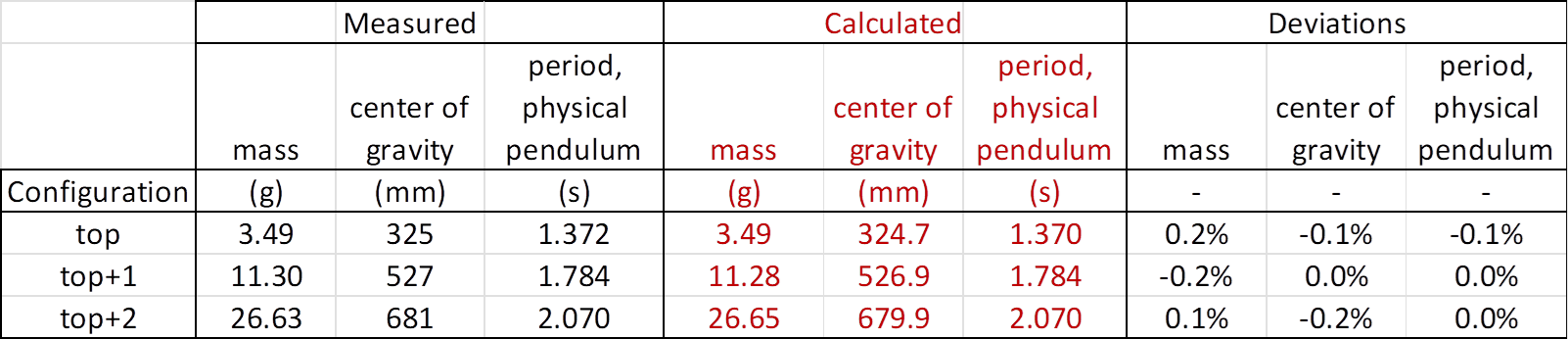
Note: The mass properties for the lower (butt) section of the rod blank isn’t possible to measure accurately. However, the sensitivity of results for complete simulations to variations in mass for the butt-section is small.

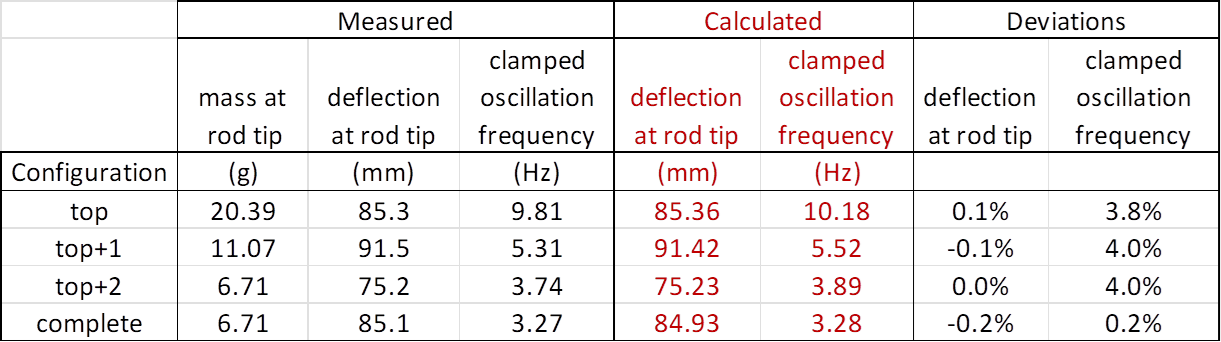
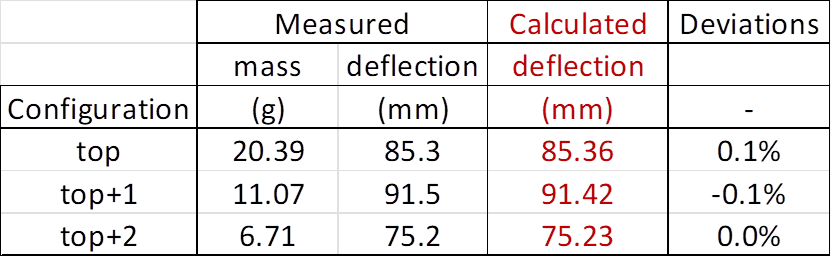
Results, rod stiffness:

Comparisons of experimental data and results from the simulation model for static deflections on rod sections are shown in the table below:

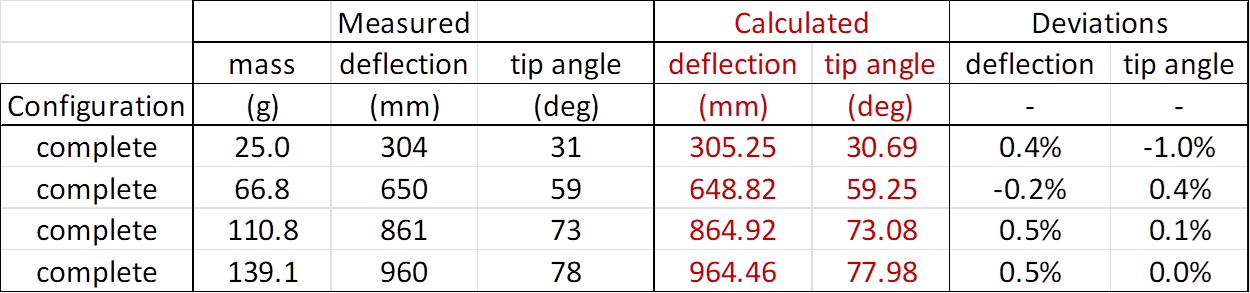
Comparisons of experimental data and results from the simulation model for deflections and tip angles for the complete rod are shown in the table below:

The calculated tip mass and tip angle versus tip deflection are shown in the graph below with the measured points from the table above:

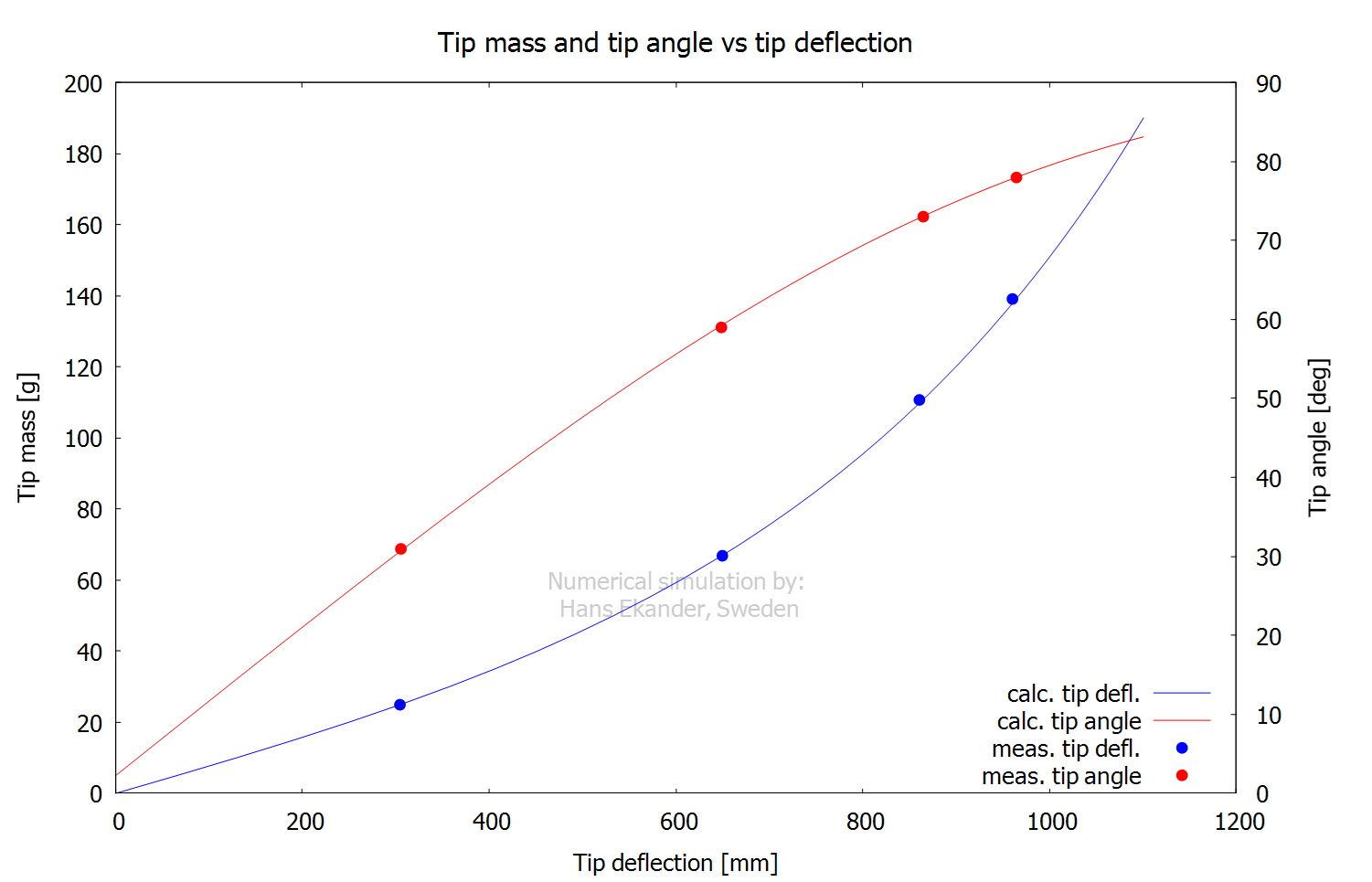
Notes:

· The graph shows the non-linear rod characteristics i.e.; the slope of the tip mass changes about a factor 5 when the deflection increases from small values to about 1 m (order of deflection for casts).

· Applying the “common cents” method gives an effective line number, ELN, for this rod of 5.0 (in agreement with the rod label).

Results, eigenfrequencies:

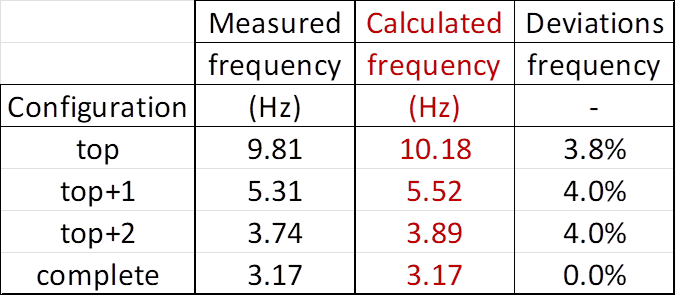
Comparisons of experimental data and results from the simulation model for the lowest eigenfrequencies of small amplitude oscillations are presented in the table below:

Conclusions:

· The calculated mass distribution shows agreement with measurements within about 0.2%.

· The calculated static deflections shows agreement with measurements within about 0.5%.

· The calculated tip angle shows agreement with measurements within about 1.0%.

· The calculated eigenfrequencies deviate up to 4% from the measurement. The deviations may be partly explained by the physical clamping not being perfectly rigid (as is the case for the calculated frequencies).

· The agreement between the experiments and the simulated rod model is concluded to be satisfactory.