Home About Basics Casts Theory Verification
References
Contact
Verification, falling horizontal
“line”
Purpose
Method
The vertical position and speed of a horizontal line falling
from rest is determined by the following three types of forces: inertia forces
(mass times acceleration), gravity forces and air drag forces. Initially, the
force balance is dominated by gravity forces and inertia forces. As the speed
increases, the relative magnitude of the air drag force will increase until it
equals the gravity force, and a “terminal” speed is reached.
Lines used in fly casting i.e., fly lines and monofilament
lines, are difficult to study experimentally since the “memory” inherent in
these lines makes them curl as soon as the ends are “let free” (internal
tension is required to keep them straight). To verify the simulation model
applied on a horizontal line falling from rest, a larger diameter
“line/cylinder” was chosen. The “line/cylinder” used, was a piece of a “pool
noodle”. The benefits of using a pool noodle were
that:
· The “line” stayed nearly straight and horizontal during the free
fall.
· The terminal speed is low (about 3 m/s)
and the “line” will almost reach its terminal speed within a 2 m fall.
· Visibility of the pool noodle, in combination with the speeds
and dimensions involved, made it possible to capture the vertical positions
versus time using a video camera and a measuring tape, see frame below.

The drawbacks of using the pool noodle
were that:
· The finite length introduces some end effects. The air drag per
unit length is decreased near the ends compared to the
center. This effect was accounted for by reducing the air drag in the
simulation model.
· The Reynolds number in the experiment becomes higher than what
is typical during fly casting. This difference was not considered critical for
the verification because the flow pattern is similar for both Re (well below
critical) and the drag coefficient is altered only about 5%, ref. “S. F.
Hoerner, Fluid dynamic drag, , 1992. Bakersfield CA:
Hoerner Fluid Dynamics”.
The measured data for the pool noodle is
listed below:
· Length: 0.798 m, Diameter:
0.059 m, Mass 26.65 g
· Mass/unit length: 0.0334 kg/m, Length/Diameter: 13.5
The account for end effects is based on data
from “Fluid Dynamics and Heat Transfer, Knudsen J. G. & Katz D. L., New York:
McGraw-Hill, 1958”. For a cylinder with L/D=13.5 the average drag per unit
length in the simulation was set to 87% of the drag for an infinitely long
cylinder.
Acknowledgement:
Henry Mittel of Long Beach Casting Club has
contributed to designing and conducting the experiments. This is gratefully
acknowledged.
Results:
Two experiments using the same set-up were
conducted. The results from them are denoted drop 1 and drop 2 respectively.
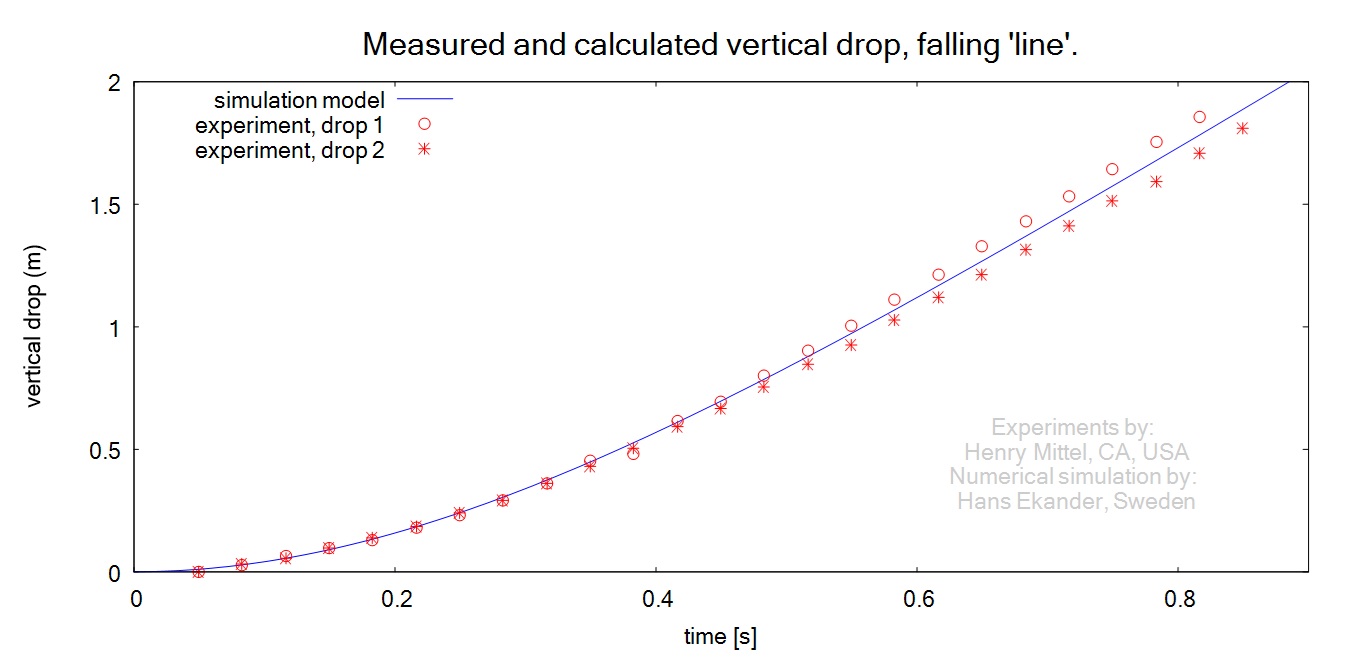
The results for the measured and calculated vertical positions versus time are
presented below:
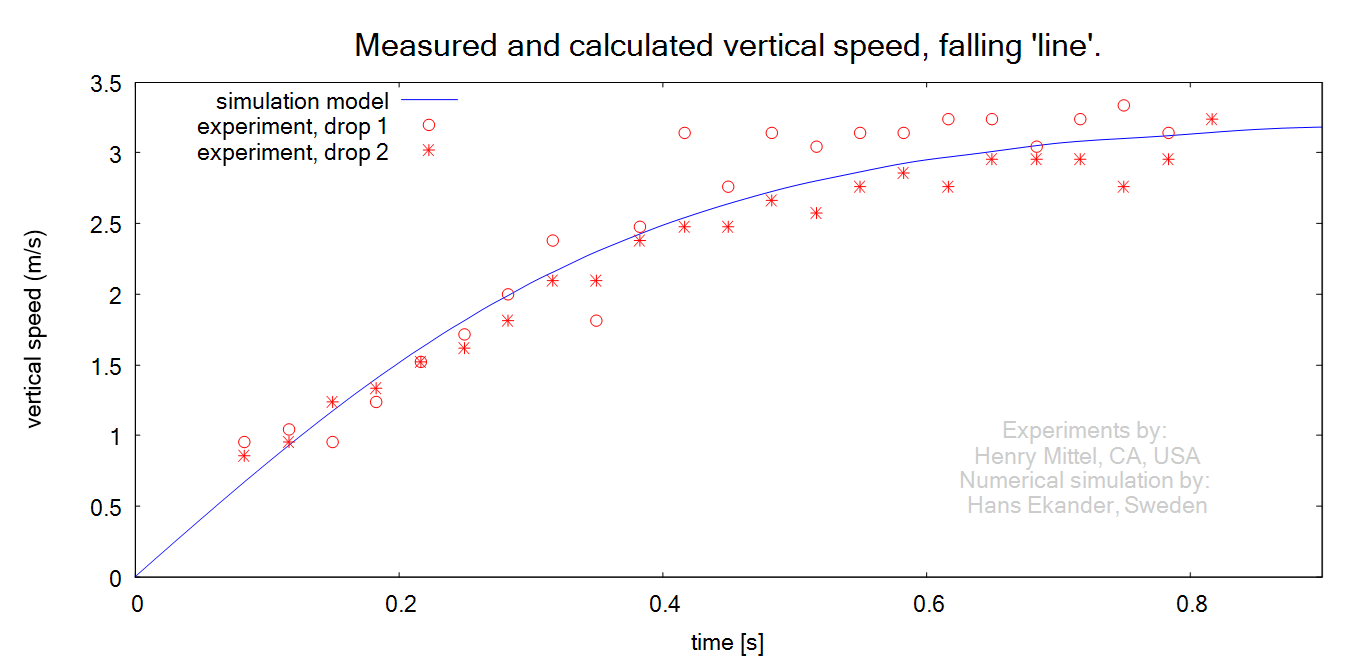
Speeds for the experiments have been obtained
by differentiating the measured positions with respect to time. The results are
presented below as is the calculated speed:
Conclusions:
· The simulation model shows that at time
0.8 s the vertical speed is about 97% of the terminal speed. Hence, the
relative contribution from inertia forces is about 1-0.972 = 6% at
the end of the experiments. This shows that at the end of the experiments, air drag force almost balances gravity force.
· The agreement between experiments and simulations is within the
spread in the experimental data. This holds for initial times (when air drag is
small) as well as final times (when air drag is dominating).
· The spread in experimental speed data is increased in comparison
to the spread in position/drop. This is explained by the differentiation
required to obtain speed from measured positions.
· The agreement demonstrates, within the accuracy of the
experiment, that the simulation model uses correct normal friction coefficients
based on the line’s diameter, air properties and instantaneous speed.