Home About Basics Casts Theory Verification References Contact

50ft oh cast, reference

Purpose

The purposes of this section are to illustrate:

· Input defining the casting stroke: angular and translational motions.

· Input defining the equipment: rod, line and fly.

· How simulated casts are animated.

· Additional output data of relevance.

At the bottom of this page some of the applied notation is explained.

Input, casting stroke

The casting stroke, i.e. the action by caster, provides input to the simulation model. The casting stroke refers to rod rotation, rod translation and line haul (if present).

The rod rotation at the handle for the 50ft ref. cast is shown below with the angle (in relation to the horizontal) and the angular velocity versus time:

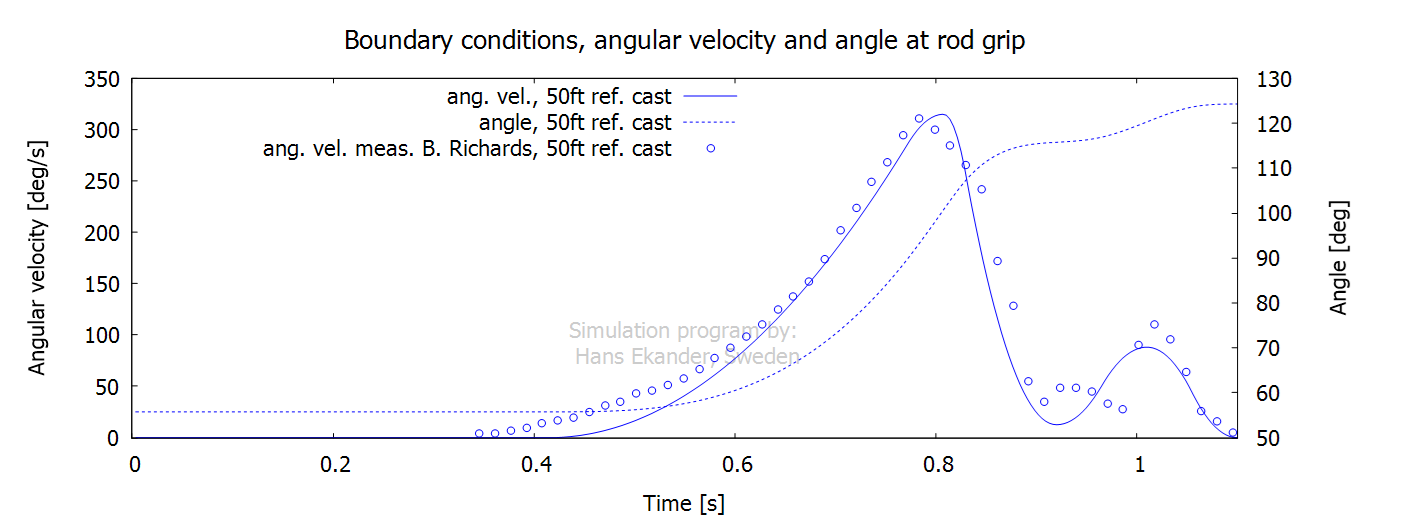
Notes:

· “Acceleration phase” refers to the time with increasing angular velocity, 0.42 to 0.81 s, above.

· “Deceleration phase” refers to the time with decreasing angular velocity, 0.81 to 0.92 s, above.

· The time from 0.92 to 1.10 s above, is referred to as “rebound and counter flex”.

· The angle and the angular velocity given as input have been set to approximately match a measured 50ft cast by the expert caster Bruce Richards.

In addition to rod rotation, the rod is usually subject to translational motion and in some cases also to line haul. The translation may be both horizontal and vertical. The casting stroke for this 50ft ref. cast is subject to horizontal translation only. The horizontal velocity (linear in contrast to the angular velocity) is shown with the angular velocity as reference below:

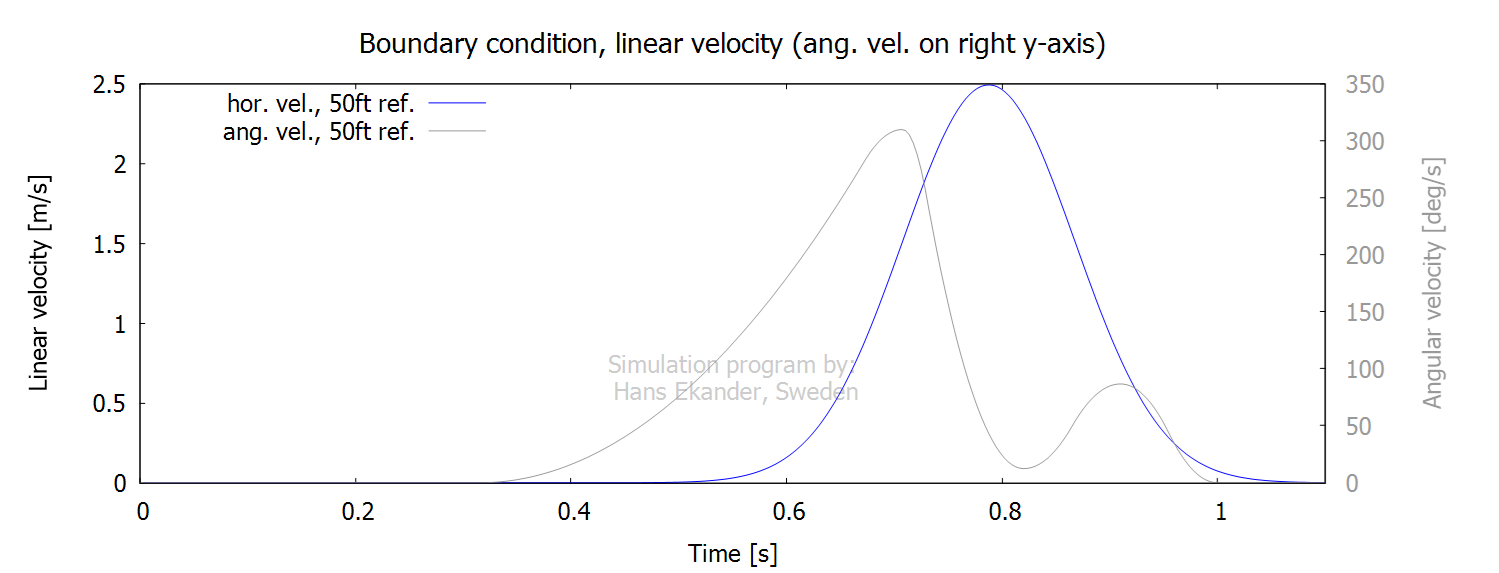
Input, equipment

The input data used to model a modern fast “high end” 5wt rod is presented below. The model has been verified through comparisons with experiments, see Verification of fly rod. If not stated explicitly, the rod model below is used in all simulated 50ft casts.

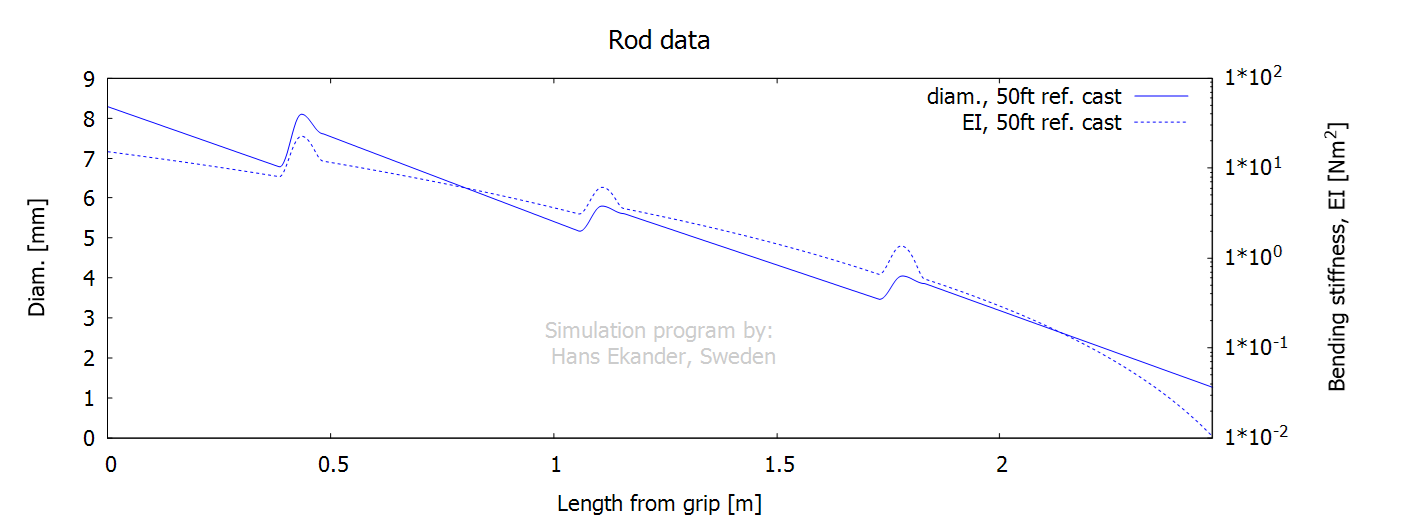
The fly rod blank is modeled for each rod section as a hollow tapered tube with a Young’s modulus and density varying linearly along each section. Each ferrule gives an increase in local bending stiffness. The outer rod diameter and the bending stiffness are presented below. Note that the outer diameter is mapped on the left axis and the bending stiffness on the right axis using a logarithmic scale.

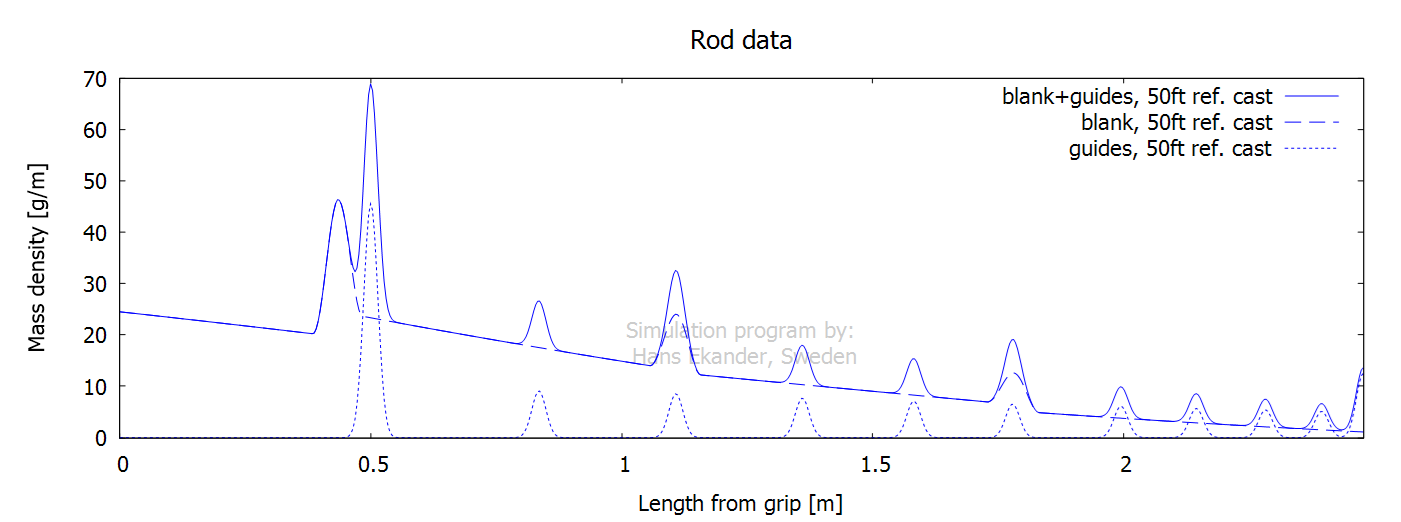
The guides (including thread & glue) give additions to the rod mass density with the relative impact being largest for the top section. The mass density for the guides is added to the mass density of the blank to give the rod mass density, see plot below:

Note: When casting, the fly line is retained to the fly rod by the guides. Therefore, the mass density of the fly line is added to the mass density of the rod in all simulated casts.

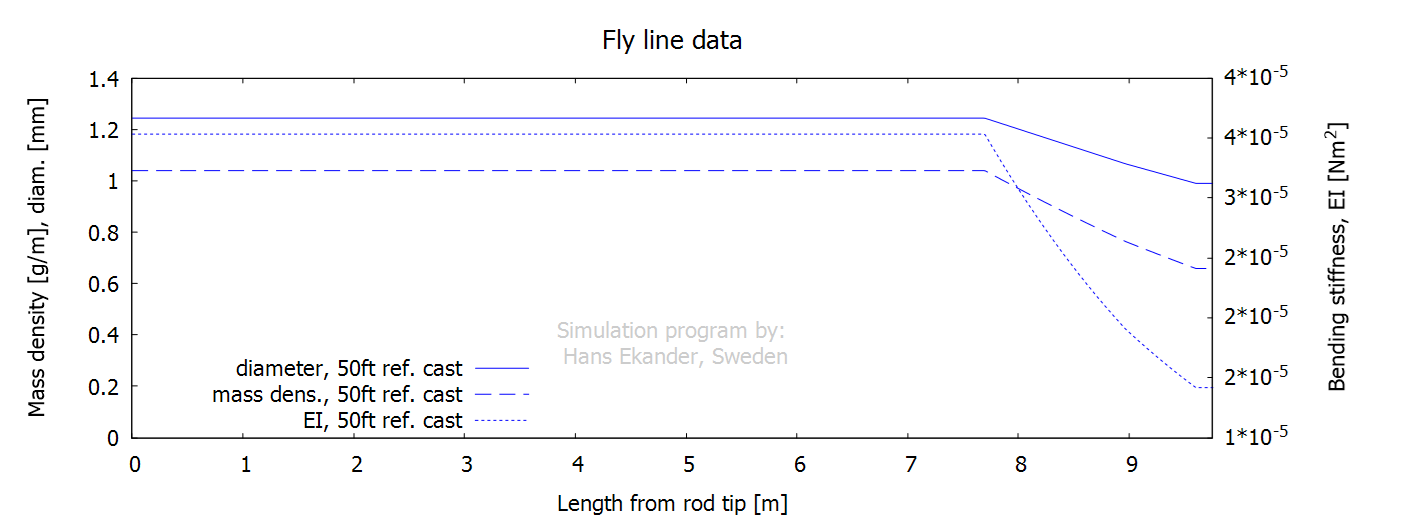
Below, the input data for the fly line and the leader (including tippet) are presented. Note that the bending stiffnesses are mapped on the right axes and that a logarithmic scale is used for the leader.

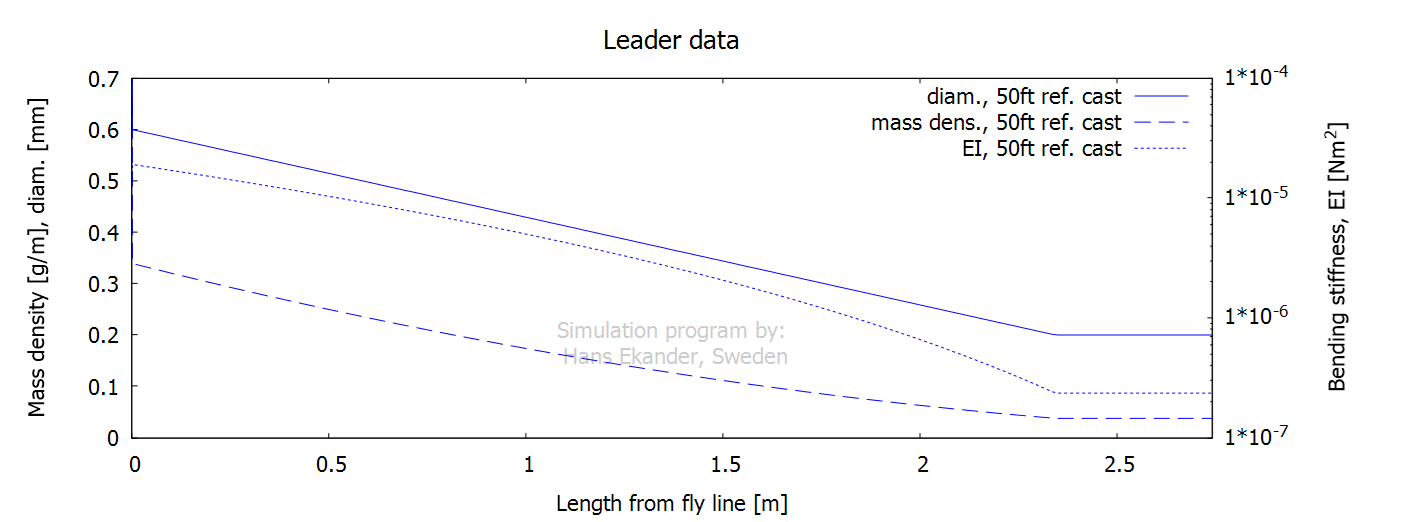
The fly attached at the end of the tippet is given a mass of 30 mg and drag giving a terminal velocity of 2.4 m/s at free fall.

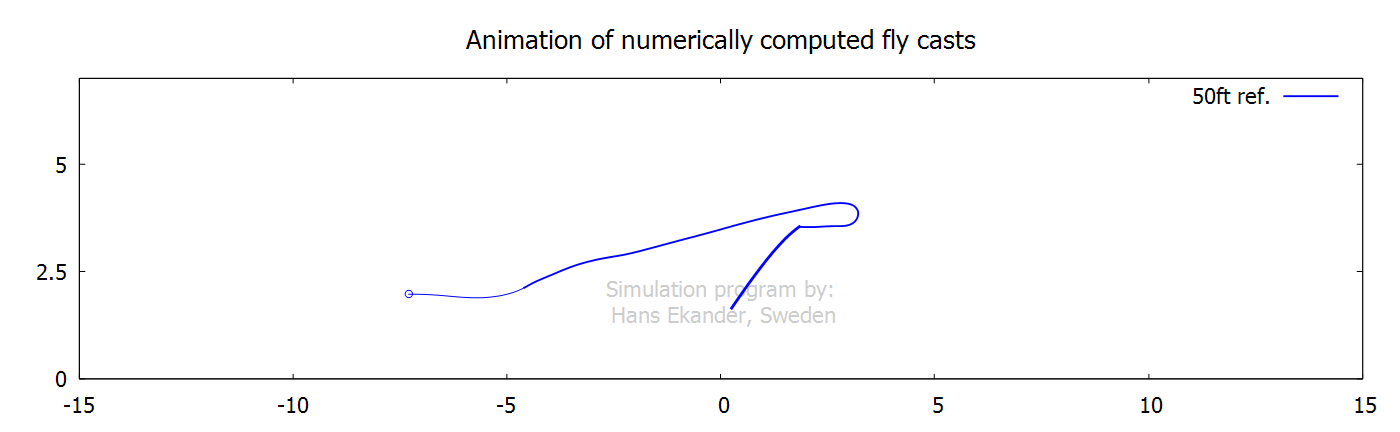
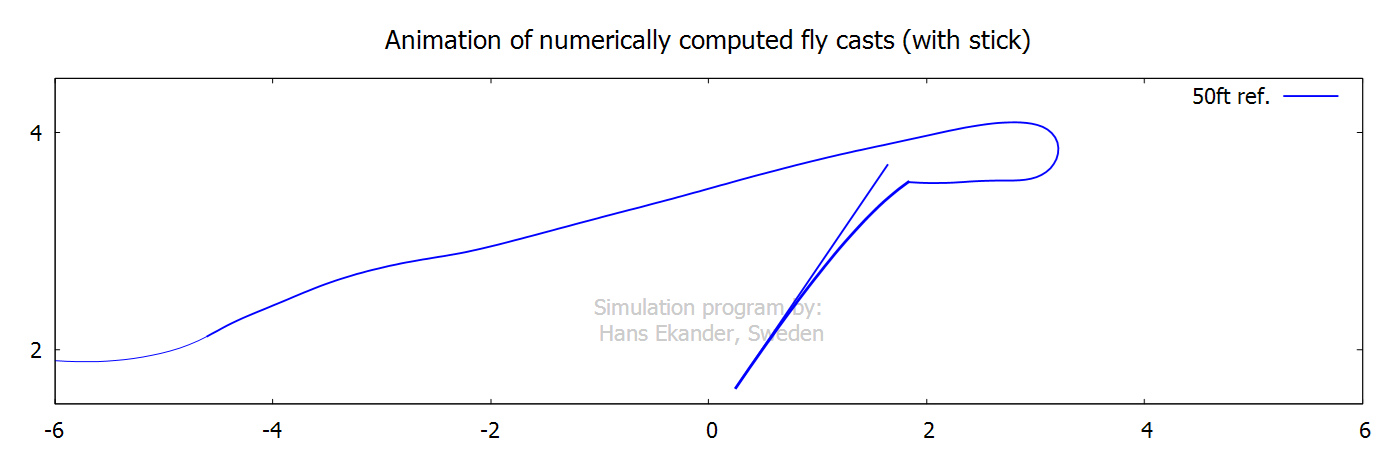
Output, animations

Click on the graphs below to start animations. Note that animations are shown in slow motion.

The animation below includes an infinitely “stiff rod” showing the rod handle movement.

Comments, animations:

The application of angular and translation velocities for the 50ft ref. cast is considered smooth. This contributes to an upper leg with limited normal air drag and wiggles. The “stiff rod” is shown “aligned with the rod handle” and shows how the rod would move if it were infinitely stiff.

Output, graphs

The graphs below are shown for one stroke (50% of a complete casting cycle).

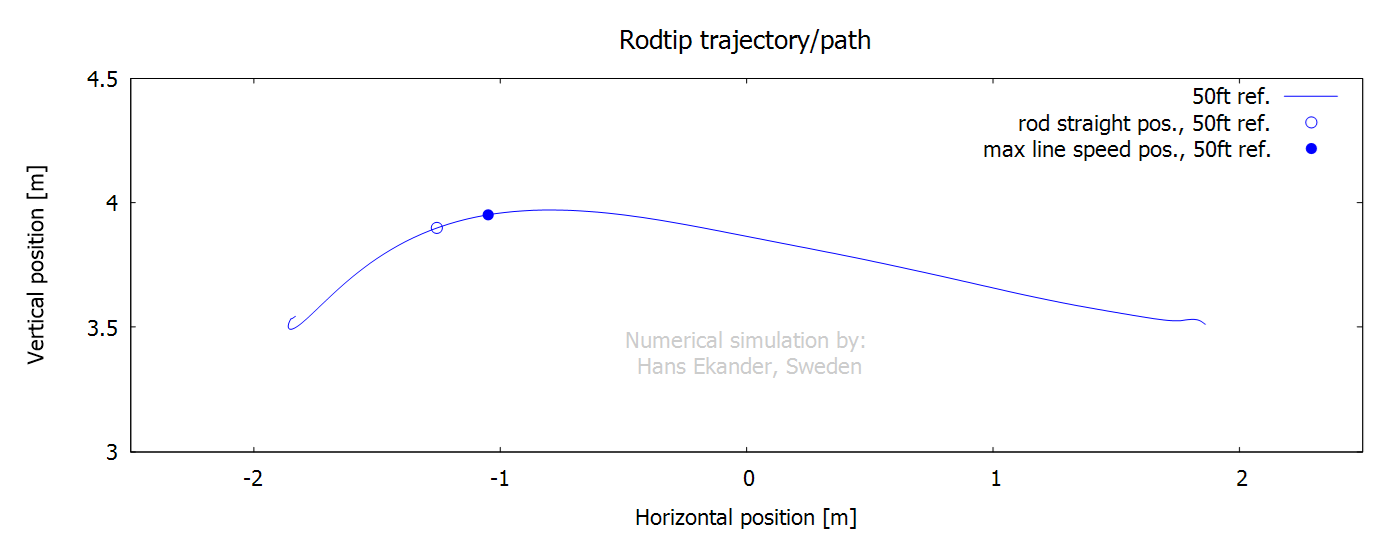
The rod tip trajectory is the path the rod tip travels (impacts loop shape). Also, shown are rod straight position (zero rod tip deflection), position of max line speed at rod tip and position for loop start (the position when the line at the rod tip is vertical). Notes:

· An excessively curved path leads to wide loops (high air drag).

· If the path has a “local dip”, that may generate a tailing loop (and line tangle).

· The vertical difference between the points “max line speed” and “loop start” reflects the loop width.

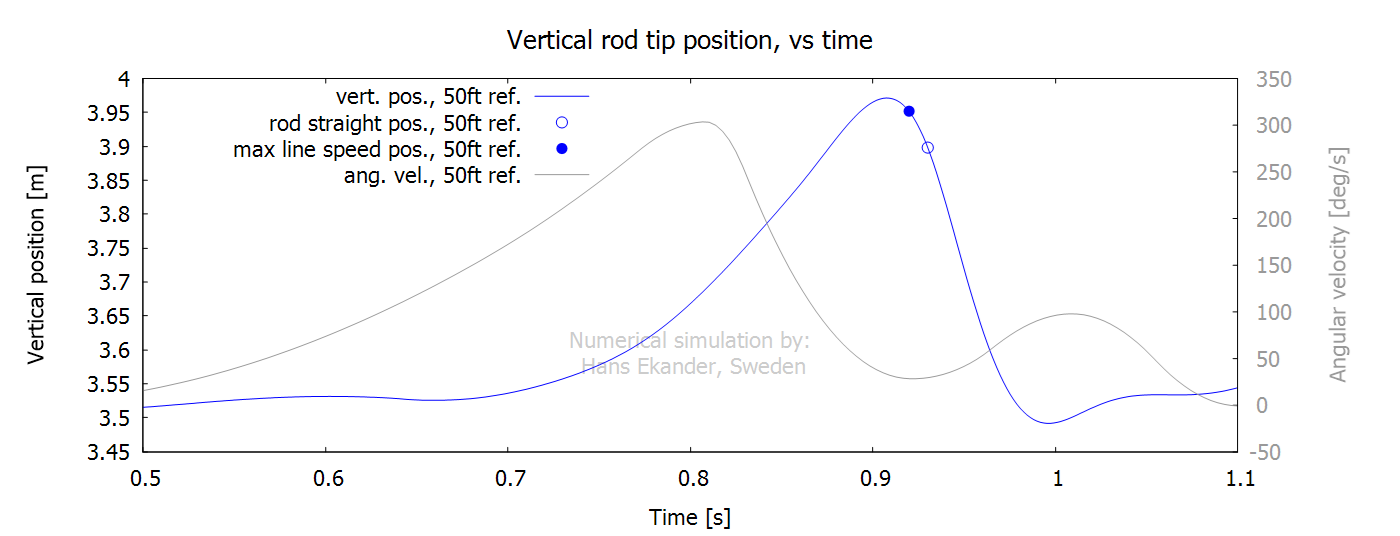
Below, the positions are shown versus time compared with the angular velocity at the rod handle.

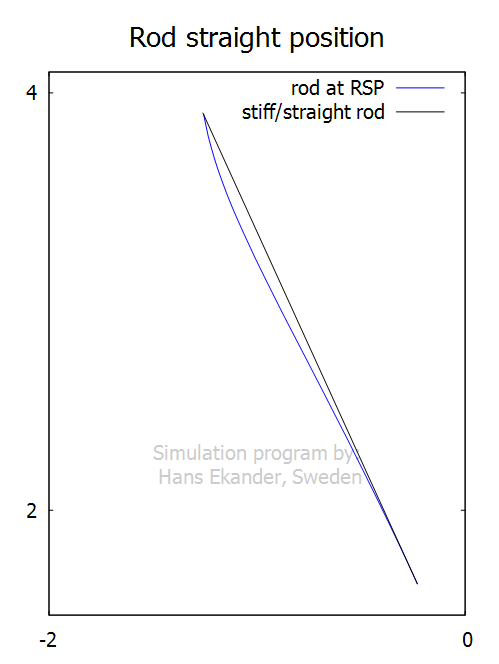
It is worth remarking on the concept of rod straight position, RSP. It is defined as the point with zero bend/deflection normal to a stiff/straight rod, but the term RSP is misleading in the sense that the rod isn’t straight. The rod shape for the cast presented in this section at the point of zero deflection is shown in the plot below:

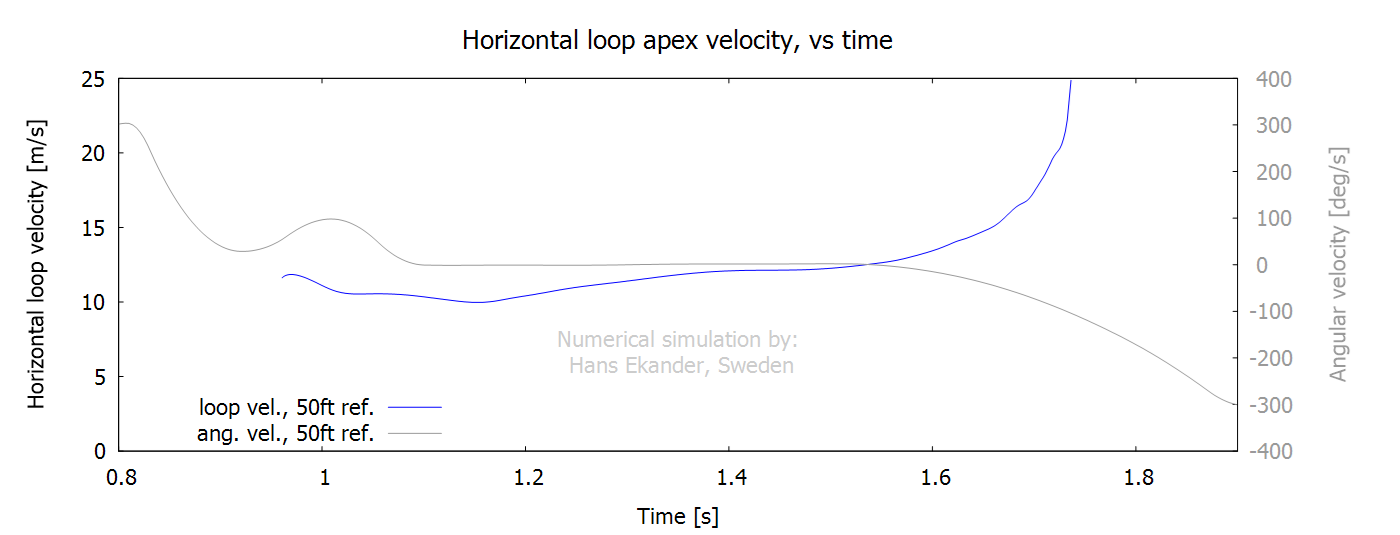
The horizontal loop velocity is the velocity of the leading edge of the fly line loop. Notes:

· The loop starts to propagate when the fly line moves “ahead” of the rod tip.

· The time window for the loop velocity differs from the other time plots below.

The radius of curvature of the fly line at the loop apex is shown below. Note:

· A larger radius indicates a wider loop (and larger normal air drag).

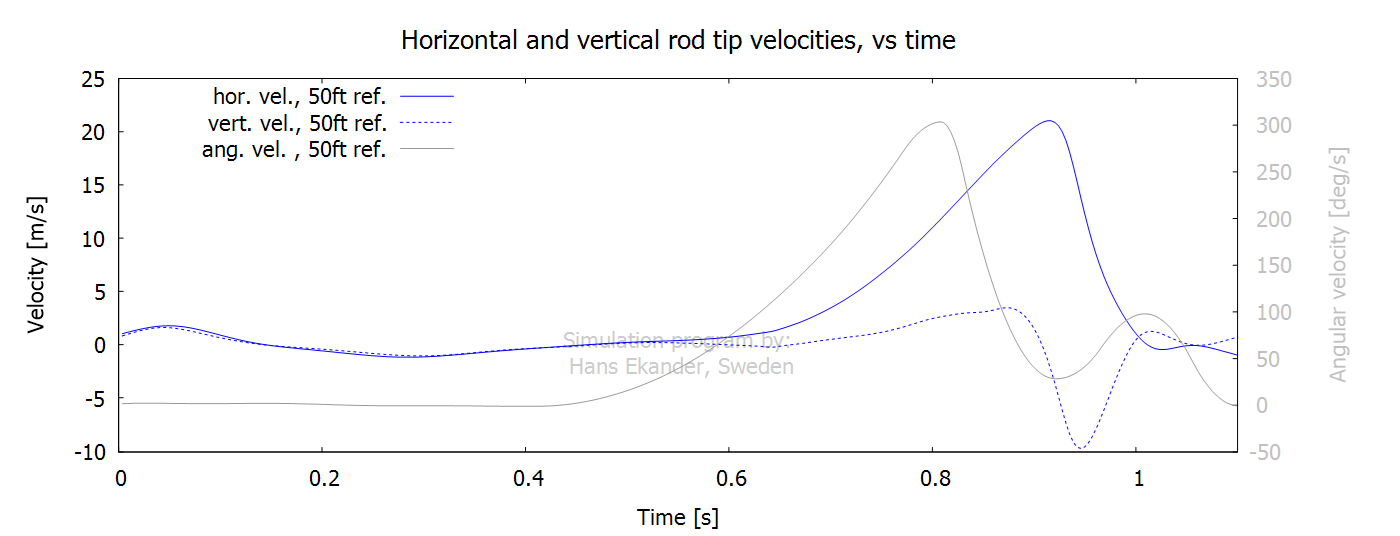
The horizontal and vertical rod tip velocities equal the respective line velocities at the rod tip (if no line haul/feed).

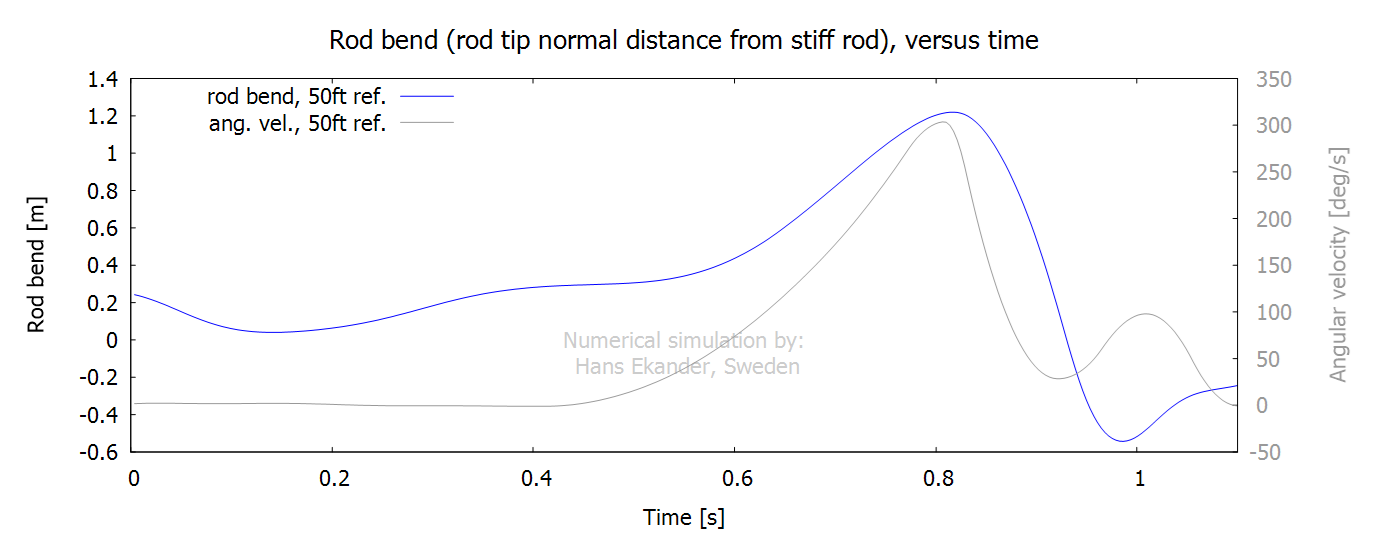
The rod bend is a measure of the rod tip deflection. It is defined as the normal distance from an infinitely stiff rod to the rod tip.

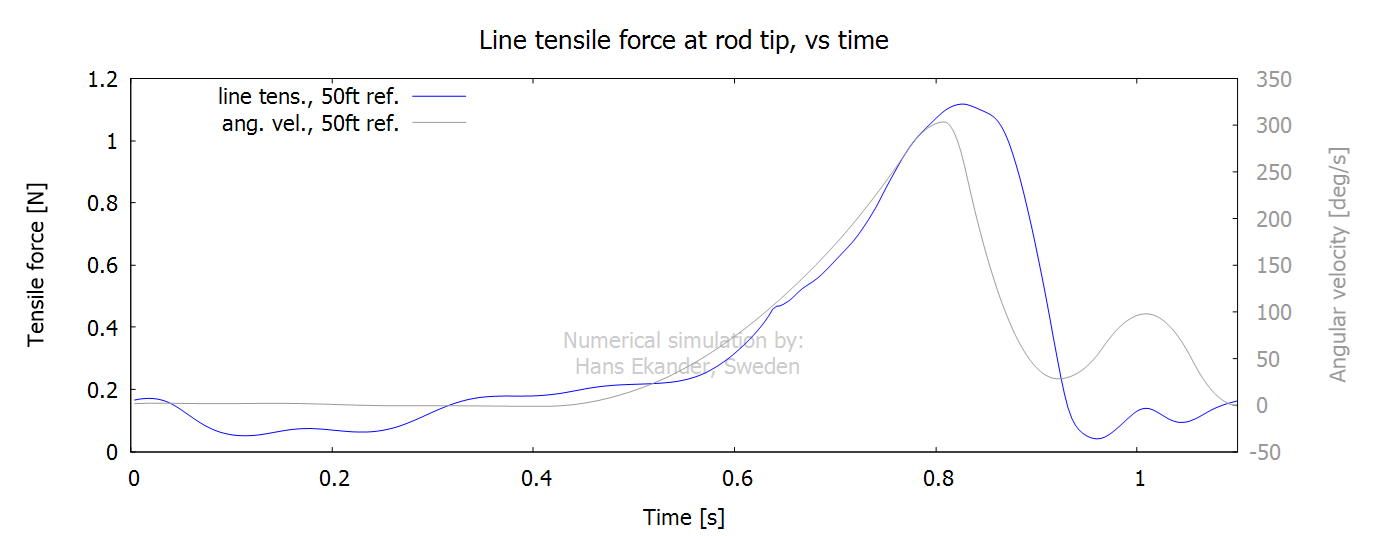
The line tensile force at rod tip is the internal line force accelerating the line.

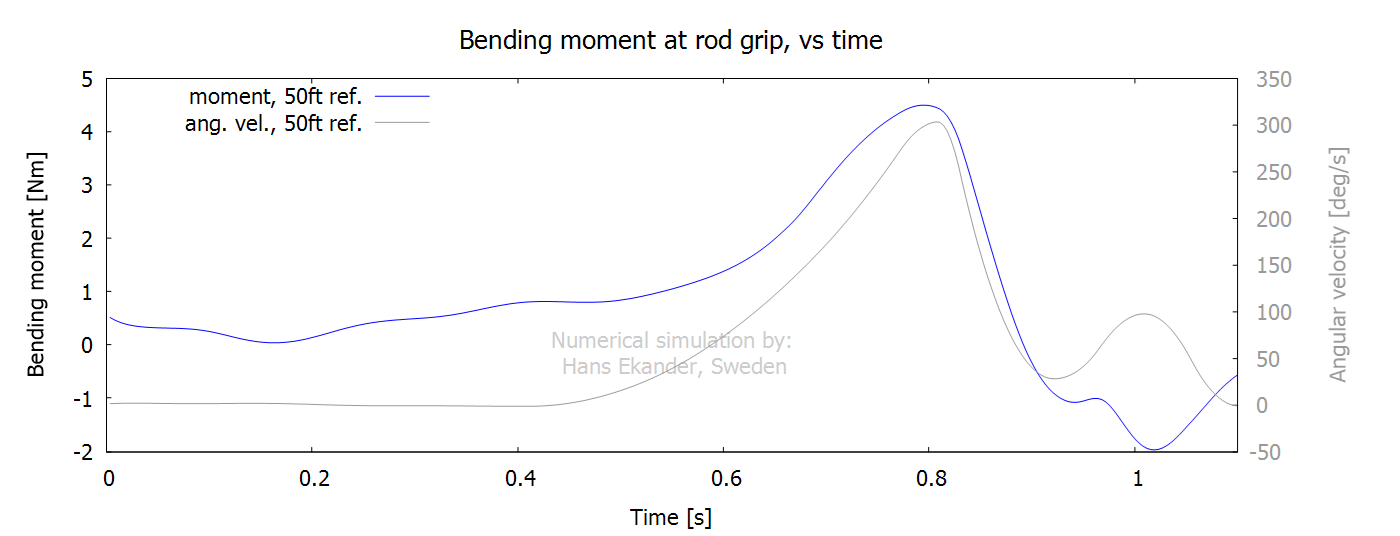
The bending moment at the rod handle gives an approximate measure of the wrist strength required by the caster. Notes:

· The bending moment in the graph below is defined at the interface between blank and handle.

· The caster’s grip is “at the handle”, so the applied bending moment by the caster isn’t exactly as the curve below.

Two forces are working to “keep the line in the air” in this cast:

1. The vertical component of the air drag.

2. The vertical component of the tensile line force at the rod tip.

The plot below shows the vertical forces working to keep the line (incl. leader and fly) in the air

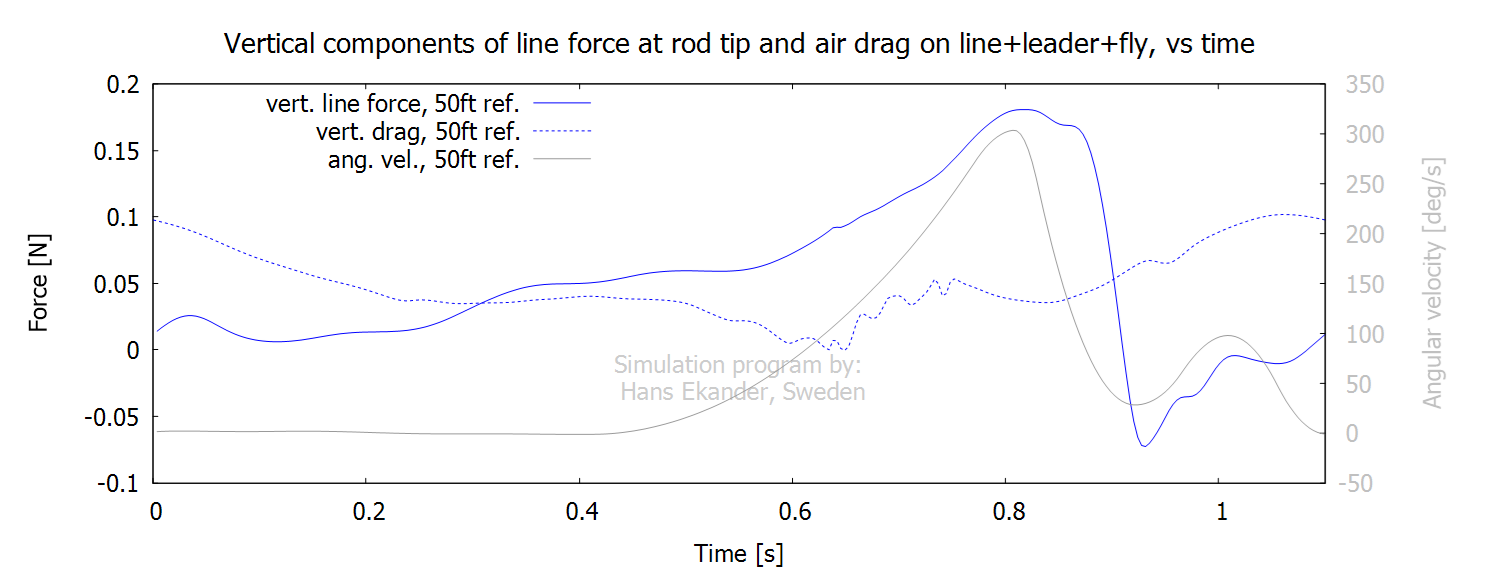
Notes:

· The time average for the vertical air drag force is about 49% of the gravity force.

· The time average of the vertical line force is about 51% of the gravity force.

· See also the vector plot of air drag force below.

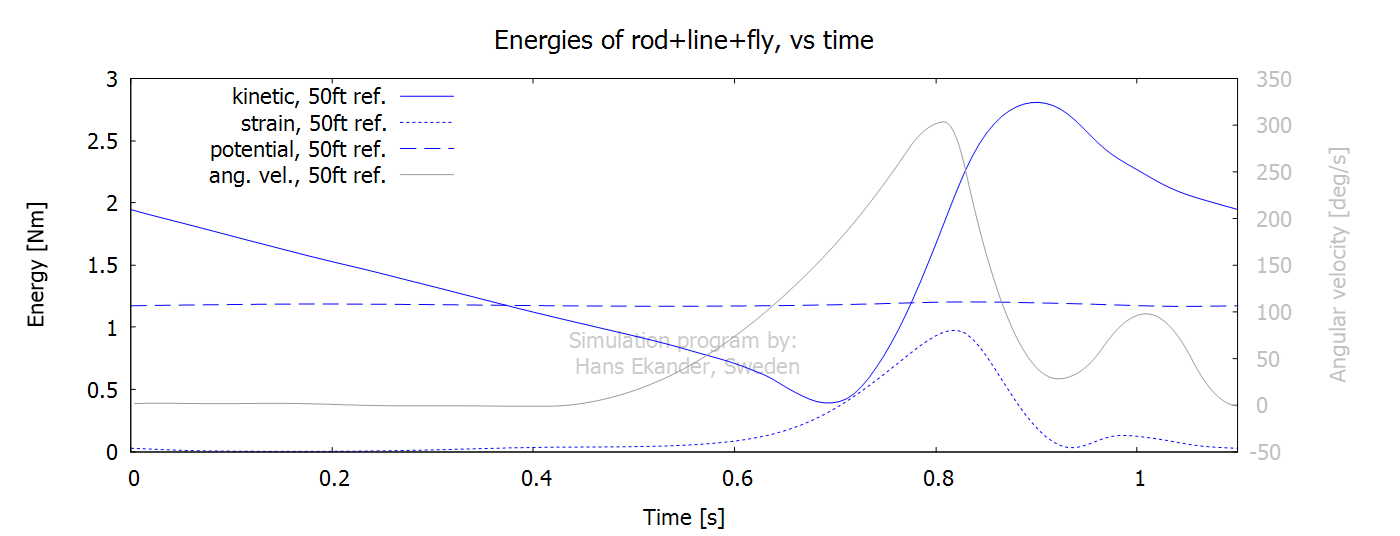
Output, energies and work

The mechanical energy in the system (here e.g.: rod+line+fly) has the following components, see the Theory section for exact definitions and “Notation” below:

1. Potential energy which is the sum/integral of the gravity force times the elevation.

2. Kinetic energy which is the sum/integral of the mass times the velocity squared / 2.

3. Strain energy which is the energy stored (mainly in the rod) due to bending. It is the sum/integral of the bending stiffness times the curvature squared / 2.

If no work is done on the system, then the conservation of mechanical energy requires that the sum of the three energy components listed above remains constant. However, if work is done on the system, then the sum of the energies will change. Here, three kinds of work are present, see the Theory section for exact definitions:

1. Work by the caster. The caster does work both due to rotation and translation of the rod handle (and due to haul, if present).

2. Work by air drag forces. Air drag is always acting to decrease the energy in the system and is referred to as loss/dissipation.

3. Work by material damping is always acting to decrease the energy in the system. Here, material damping is present when the curvature/bending changes (mainly in the rod).

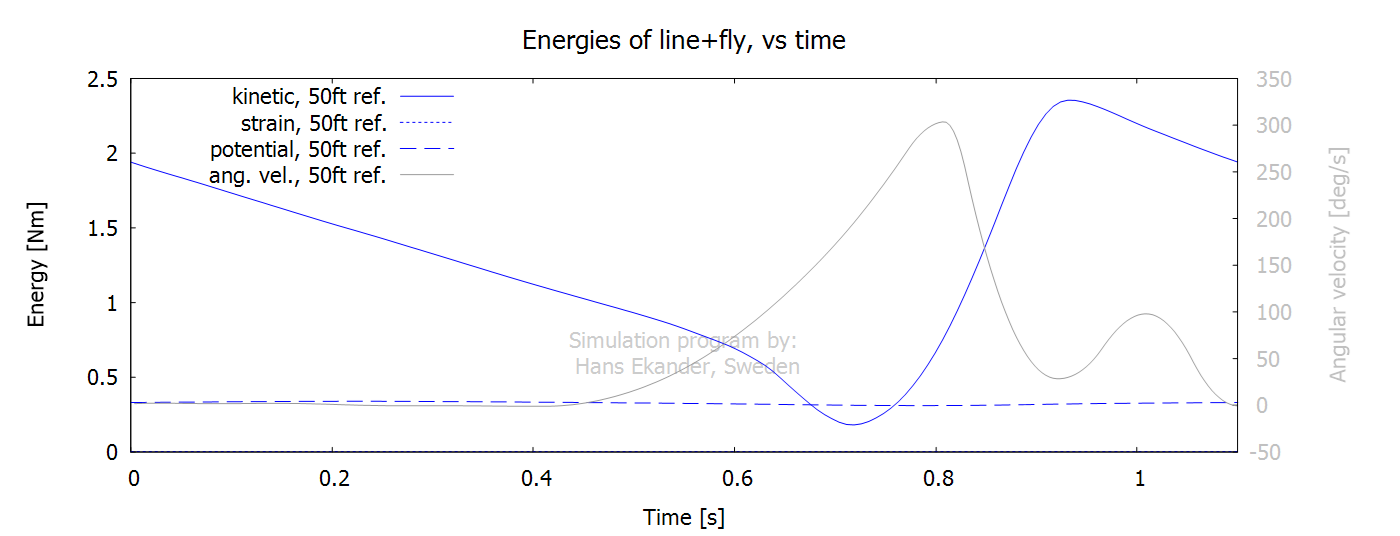
The energies presented below include rod+line+leader+fly. Note:

· For symmetric casts, as the one shown here, the energies at the start and end of each stroke are equal.

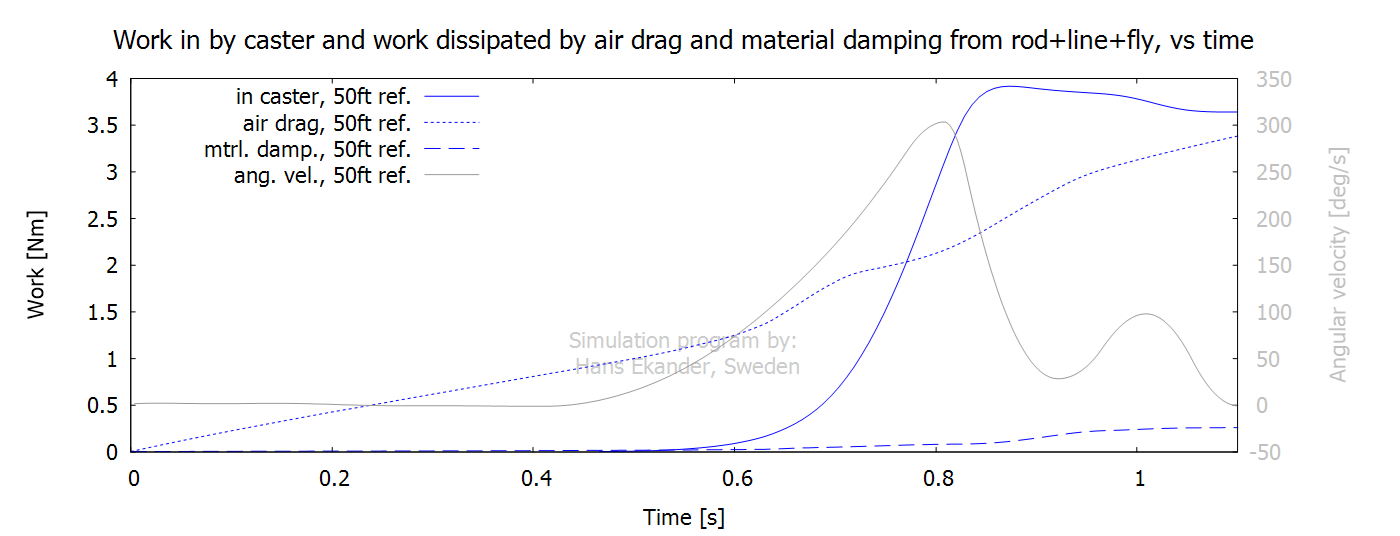
The cumulative work (from start) by fluid drag and material damping, presented below, include rod+line+leader+fly. Notes:

· The sum of the accumulated dissipated work by air drag and material damping equals the accumulated work input by the caster at the end of the stroke. Hence, the net work done on the system is zero, consistent with the energy being the same at the start and end of the symmetric cast.

· Mechanical work in by the caster decreases at the end of the stroke. The accumulated muscular effort, however, increases throughout the entire stroke.

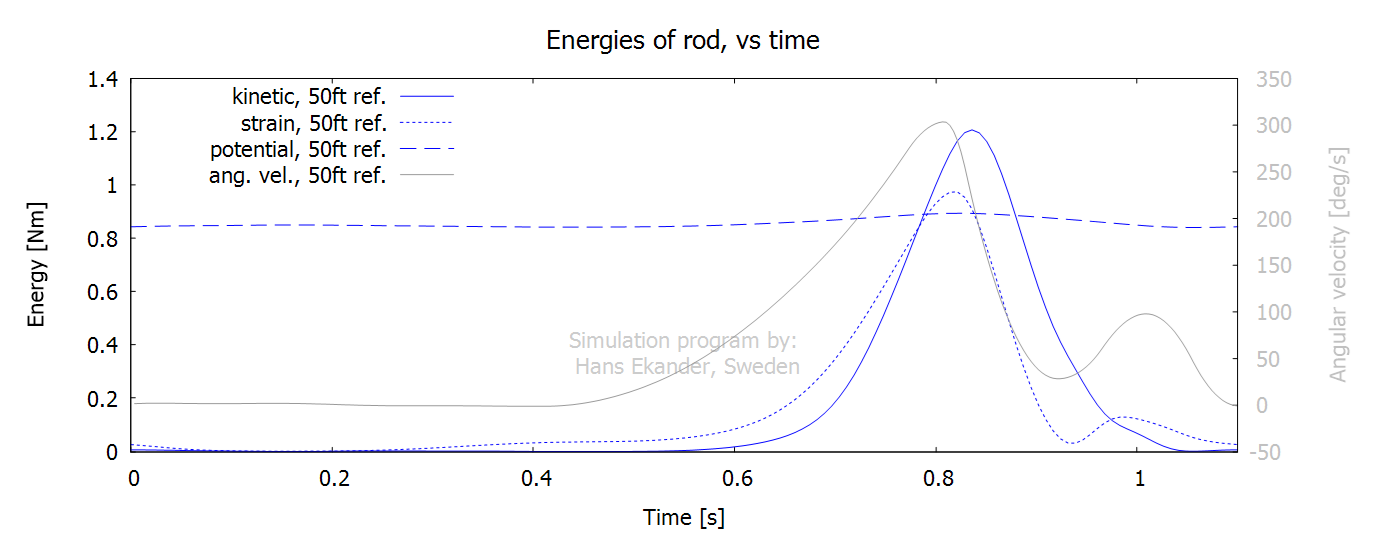
The energies for the rod only are presented below.

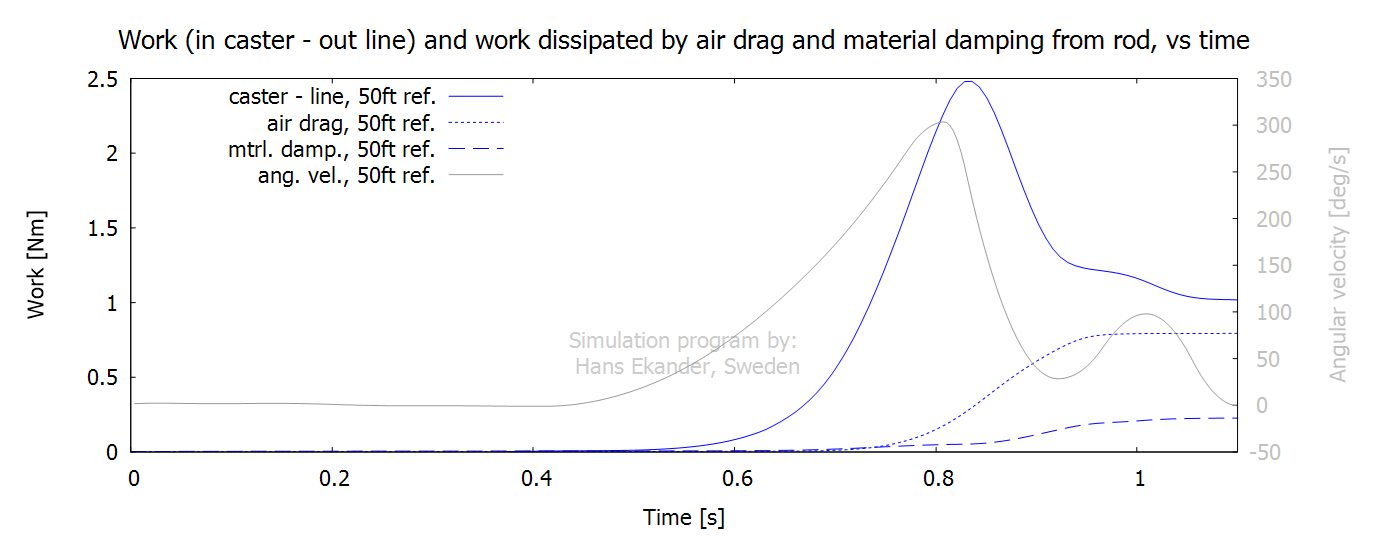
The cumulative work (from start) for the rod only by fluid drag and material damping are shown below. Note:

· “caster-line” is the accumulated work input by the caster minus the accumulated work done by the rod on the fly line (at the rod tip).

The energies for the line (incl. leader) and fly are presented below.

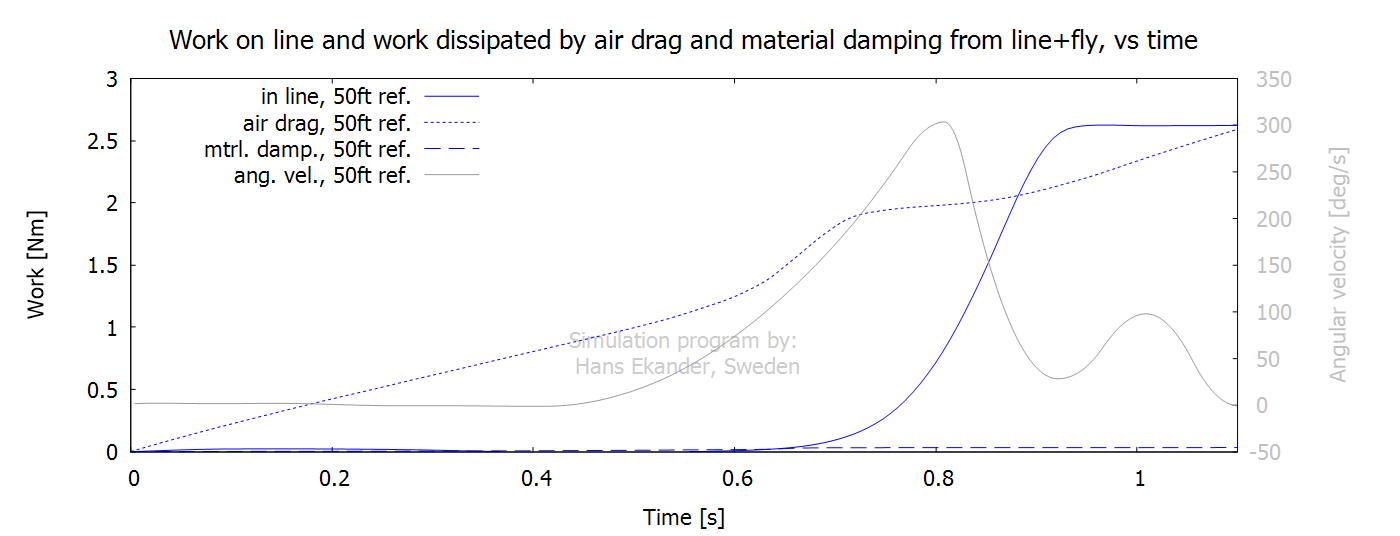
The cumulative work (from start) for the line (incl. leader) and fly by fluid drag and material damping are shown below. Note:

· “in line” is the accumulated work done by the rod on the fly line (at the rod tip).

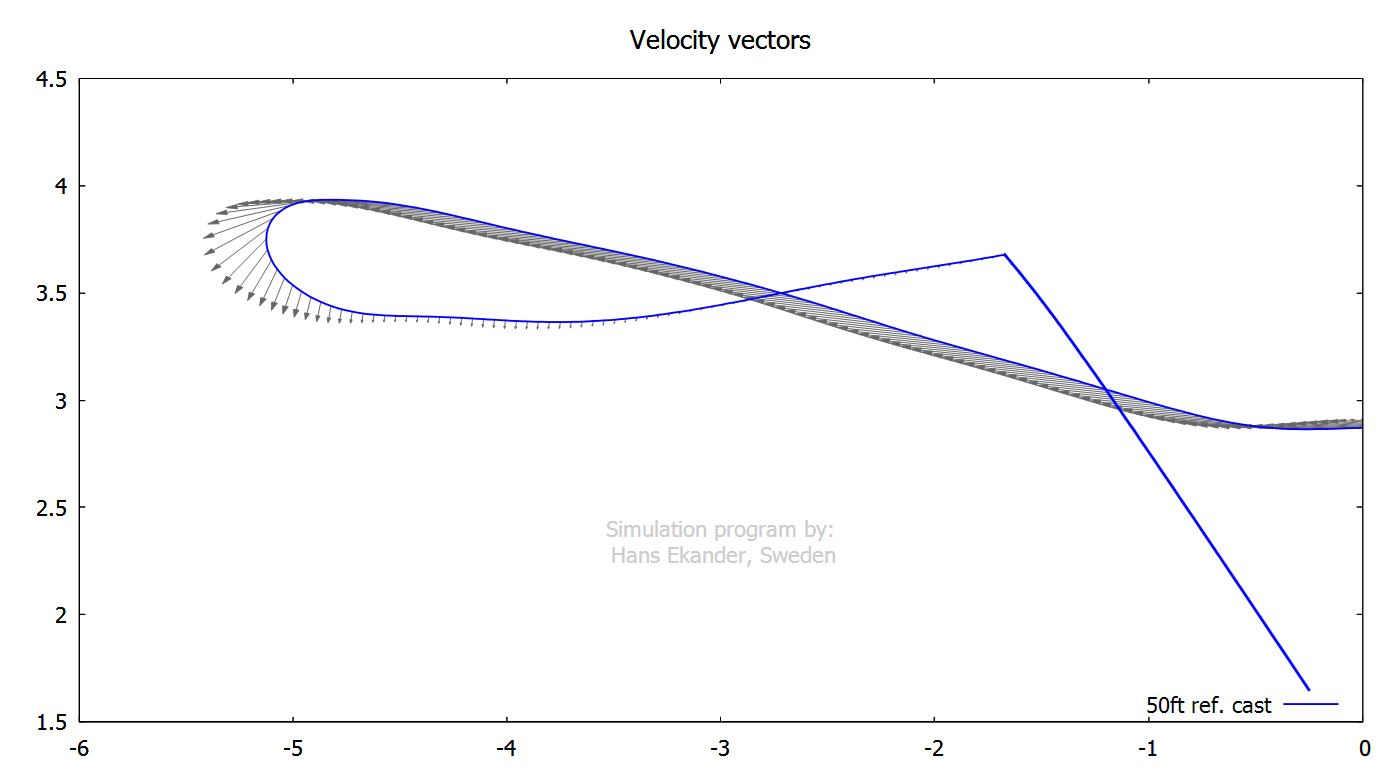
Output, vectors

The vector plot below shows the local velocity when the loop has propagated about a rod length. Note that the loop front velocity is not identical with the line velocity.

The vector plot below shows the local air drag force per unit length. Notes:

· The axial air drag is only about 2% of the normal air drag (for equal axial and normal velocities).

· The integrated air drag generates a net “lift”.

The vector plot below shows the internal force vectors.

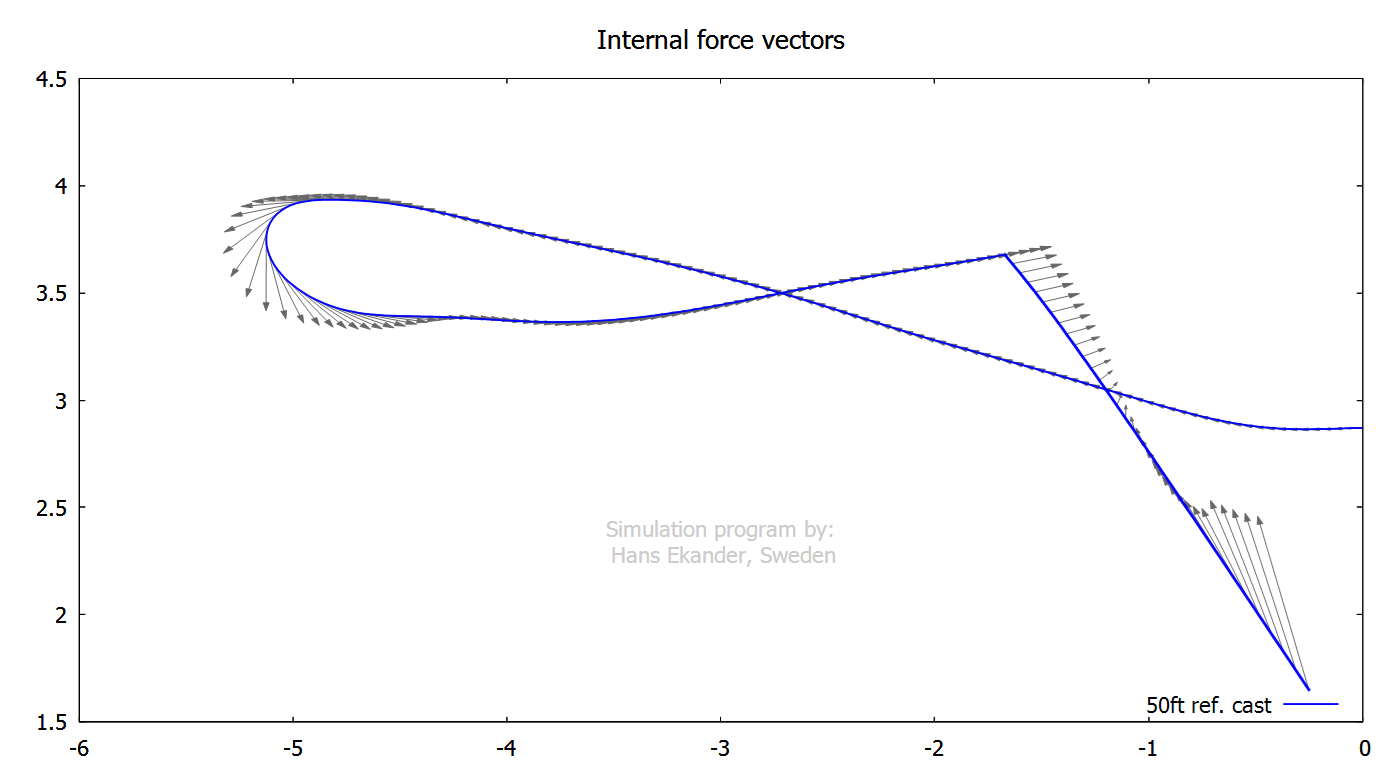
Notation, see also Theory:

Speed A measure of how fast an object is moving, in units of length/time.

Velocity Speed in a specific direction, in units of length/time.

Haul velocity Line speed through the guides toward the rod handle.

Feed velocity Line speed through the guides toward the rod tip.

Acceleration The rate of change of the velocity of an object with respect to time.

Angular velocity Velocity of rotation around a point, in units of angle/time.

Boundary condition Conditions that are defined/set at either end of the computation domain e.g., at the rod handle or at the fly.

Young’s modulus Is a measure of the stiffness of a material defined as stress/strain, in units of force/area. Stress is the force per unit area and strain is the elongation/length.

Curvature The curvature of an element, e.g. the rod or the line, is 1/(radius of curvature) and it is measured the unit of 1/length.

Bending moment Bending moment is the reaction induced in a structure, e.g. the rod, when it is loaded in such a way as to making it bend, measured units of force*length.

Bending stiffness The bending stiffness, here denoted EI, is a measure of the resistance of a slender structure, here the rod or the line, to bend. EI = (bending moment)/curvature.

Mass density Mass density is measured in units of mass/length. The mass density is the mass of a very short piece (of rod or line) divided by the length of the very short piece.